OBJECTIVE: To compare the shoulder load during handcycling and wheelchair propulsion under similar conditions of external power in persons with spinal cord injury.
DESIGN: Cross-sectional.
SUBJECTS: Eight men with spinal cord injury.
METHODS: Kinetics and kinematics were measured during handbike and wheelchair propulsion at 25, 35, 45 and 55 W on a treadmill. Shoulder load (glenohumeral contact forces, relative muscle forces) was calculated with the Delft Shoulder and Elbow Model.
RESULTS: At all power output levels, glenohumeral contact forces were significantly lower during handcycling compared with wheelchair propulsion (p < 0.001). At 55 W, the mean glenohumeral contact force was 345 N for handcycling, whereas it was 585 N for wheelchair propulsion. Also, relative muscle forces were lower during handcycling. The largest differences between handbike and wheelchair propulsion were found in the supraspinatus (4.5% vs. 20.7%), infraspinatus (3.7% vs. 16.5%) and biceps (5.0% vs. 17.7%).
CONCLUSION: Due to continuous force application in handcycling, shoulder load was lower compared with wheelchair propulsion. Furthermore, muscles that are prone to overuse injuries were less stressed during handcycling. Therefore, handcycling may be a good alternative for outdoor mobility and may help prevent overuse injuries of the shoulder complex.
Key words: mobility; handbike; wheelchair; biomechanics; muscles; rehabilitation; shoulder; spinal cord injury.
J Rehabil Med 2011; 00:00–00
Correspondence address: Ursina Arnet, Swiss Paraplegic Research, Guido A. Zächstrasse 4, CH-6207 Nottwil, Switzerland. E-mail: ursina.arnet@paranet.ch
Submitted May 18, 2011; accepted November 1, 2011
Introduction
Optimizing physical capacity and muscle strength through regular exercise is important for persons with spinal cord injury (SCI) (1). Good physical condition helps with the efforts of activities of daily living, and helps prevent long-term health problems, such as diabetes or cardiovascular disease (2). The handrim wheelchair is the device mainly used for daily mobility, as well as for sports and training purposes. However, handrim wheelchair propulsion is physiologically and mechanically straining (3, 4). The high peak forces applied to the pushrim and the repetitive forces acting on the shoulder joint have been associated with injuries of the shoulder joint, mainly overuse injuries of the rotator cuff (5). Since wheelchair propulsion is the main mode of mobility for persons with SCI, its frequent use contributes to the high prevalence of upper extremity injuries in persons with SCI (6), which range from 30% to 73% (7, 8). This prevalence of shoulder pain is 3 times higher than that of the general population (9). Since persons with SCI rely on their arms for mobility and activities of daily living, shoulder pain will affect their independence, their participation in the community, and their quality of life. Therefore, there is a need to study alternative modes of wheelchair propulsion, where shoulder load, and consequently the risk for injuries of the upper extremity, are expected to be lower.
The handbike is one of the alternative modes of propulsion that is increasingly used for regular exercise, and which is a good alternative to handrim wheelchair propulsion since it is more efficient and physiologically less straining (3, 10). Whether it is also a good device for the prevention of shoulder problems has not yet been investigated in detail. A recent study has quantified the shoulder load (glenohumeral contact force and relative muscle forces) of able-bodied subjects during handcycling (11). Comparison of the results with findings from earlier studies of wheelchair propulsion (12, 13) has shown that the shoulder load is lower during handcycling. These findings should be verified in a direct comparison between handcycling and handrim wheelchair propulsion in the SCI population. The aim of the present study is to compare the shoulder load during handcycling and wheelchair propulsion in persons with SCI. Shoulder load will be calculated using a biomechanical model and quantified as joint and muscular load. Previous studies on mechanical load during handcycling and handrim wheelchair propulsion suggest that both joint and muscular load will be lower during handcycling.
Methods
Subjects
After providing written informed consent, 8 men with paraplegia participated in this study. Subjects were eligible to participate if they perform handbike sports on a weekly basis. Exclusion criteria were current shoulder complaints or previous shoulder surgery. Subjects’ characteristics are listed in Table I. The study was approved by the local ethics committee.
| Table I. Characteristics of the 8 subjects with spinal cord injury |
| Subjects | Age, years | Weight, kg | Height, m | Time since injury, years | Heart rate rest, bpm | Training, h/week | AIS score | Lesion level | Used wheelchair |
| 1 | 47 | 76 | 1.70 | 11 | 49 | 18 | C | L1 | Own |
| 2 | 43 | 70 | 1.78 | 23 | 80 | 1 | A | Th4–5 | Lab |
| 3 | 25 | 79 | 1.70 | 25 | 82 | 14 | A | L3–4 | Lab |
| 4 | 39 | 73 | 1.84 | 19 | 94 | 5 | A | Th4–5 | Own |
| 5 | 35 | 66 | 1.86 | 9 | 84 | 6 | A | Th2 | Own |
| 6 | 29 | 95 | 1.87 | 9 | 70 | 2 | A | Th4 | Lab |
| 7 | 41 | 86 | 1.85 | 6 | 80 | 3 | A | Th4 | Lab |
| 8 | 47 | 85 | 1.79 | 31 | 68 | 13 | A | Th2 | Own |
| Mean (SD) | 38 (8) | 79 (1) | 1.80 (0.07) | 17 (9) | 76 (14) | 10 (8) | | | |
| SD: standard deviation; AIS: ASIA Impairment Scale. |
Experimental design
After familiarization with the experimental procedure and set-up, subjects propelled the handbike (Fig. 1) and the wheelchair on a motor-driven treadmill (Mill, Forcelink BV, Culemborg, The Netherlands) at power output levels of 25, 35, 45 and 55 W, regulated with a pulley system (14). The individual drag force, to define the extra weight acting on the pulley system, was determined in a separate drag test (15).
The duration of each exercise block, at a certain power output level, was 3.5 min and data were collected during the last 30 s. Between the exercise blocks a rest period of 3 min was given.
To simulate an everyday propulsion speed, the belt velocity was set to 1.66 m/s for the handbike and 1.11 m/s for the wheelchair, similar to earlier studies (16, 17). The gear ratio of the handbike was fixed throughout the experiment at 0.741, which resulted in a cadence of 52 rpm. This cadence has been found suitable for submaximal handcycling (17).
Both propulsion devices were tested on the same day, in randomized order with a rest of 45 min in between.
Kinetics
The handbike used in these experiments was an attach-unit system (Tracker Tour, Double Performance, Gouda, The Netherlands) with a synchronous crank setting (18) (Fig. 1). The additional front crank-driven wheel was attached to a handrim wheelchair (Pro Competition, Cyclone Mobility & Fitness, Bromborough, UK). The external propulsion forces were measured on the left handle bar with a special purpose crank unit (Faculty of Human Movement Sciences, VU University, Amsterdam, The Netherlands), which recorded three-dimensional forces at 100 Hz (18). The measured forces were transformed to the local coordinate system of the crank (tangential, radial, lateral) and to forces in the global coordinate system (18). Produced external power output (POhandbike) was calculated under the assumption that equal forces were applied with the left and right hands. Power output of handcycling was calculated from the product of the tangentially applied force component and the linear velocity of the crank system: POhandbike = 2Ftanvcrank (19).
Fig. 1. Subject sitting in the handbike, with cluster markers attached to thorax, left acromion, upper arm, lower arm and hand.
The external forces during handrim wheelchair propulsion were measured with a SmartWheel (Three Rivers Holdings LLC, Mesa, Arizona, USA) in the global coordinate system at 100 Hz. If the SmartWheel fit the subject’s own wheelchair, then the experiments were performed in his wheelchair. Otherwise, the wheelchair of the laboratory was used (Küschall K-Series, Küschall AG, Witterswil, Switzerland). The wheelchairs were fitted with the SmartWheel on the left side and a dummy wheel on the contra-lateral side (16). Under the assumption that equal forces were applied with the left and right hand, power output of wheelchair propulsion (POwheelchair) was calculated from the measured moment (Mwheel) and the angular velocity (ωhandrim): POwheelchair = 2Mhandrimωwheel (20).
Kinematics
Synchronous to the kinetic data collection, the kinematics of the upper limb was recorded at 100 Hz with a 6-camera movement analysis system (Oqus, Qualisys AB, Gothenburg, Sweden). Five unique clusters of reflective markers (4 markers each) were placed on the trunk and on the upper extremity on the left-hand side (thorax, acromion, upper arm, forearm and hand; Fig. 1). Prior to the actual experiment, calibration measurements were performed in which the cluster markers were defined relative to the bony landmarks. From the cluster markers recorded during the experiment, the positions of the anatomical landmarks during the actual experiment were reconstructed, as well as the local coordinate systems of the thorax and upper extremity (21), and in line with previous studies on joint contact forces in wheelchair propulsion (12, 13).
Inverse dynamic model
Biomechanical models can be used to quantify the load on musculoskeletal structures, such as the shoulder joint (22). One of the musculoskeletal models for the upper extremities is the Delft Shoulder and Elbow model (23), which was used in the present study to calculate the shoulder load. This model can be used in an inverse-dynamic mode and consists of motion equations describing the mechanical behaviour of the upper extremity, derived by using the finite element method. The model consists of 31 muscles, divided into 139 muscle elements. For muscles with large attachment sites or with complex architecture, more than one muscle element is necessary to represent the mechanical effect of the muscle. The Delft Shoulder and Elbow model has been validated by comparing the calculated glenohumeral contact force and muscle forces with values measured using an instrumented shoulder prosthesis and electromyography recordings (24).
The input data were mirrored to the right side of the subject since the model represents a right shoulder and arm. Kinematic input was the position of the incisura jugularis, the orientations of the thorax, scapula, humerus, forearm and hand. The 3-dimensional external forces and moments applied by the hand on the crank (handbike) and the handrim (wheelchair) served as kinetic input. Output variables used in this study were the glenohumeral contact force and the relative forces of muscles that were assumed to be relevant for the shoulder load (supraspinatus, infraspinatus, subscapularis, teres minor, deltoid, triceps, teres major, trapezius, biceps, coracobrachialis, serratus and pectoralis). Glenohumeral contact forces are the sum of all forces acting on the joint, thus both external forces and muscle forces. For comparison with data from previous studies, a minimum stress cost function was used to calculate the muscle forces (25). The total force produced by each muscle was obtained by summing the forces of the muscle elements. Muscle forces were expressed as a percentage of their maximum, based on a force per physiological cross-sectional area of 100 N/cm2 (26).
Data and statistical analysis
From the last 30 s of each exercise bout, 5 regular consecutive propulsion cycles were selected for data analysis. The propulsion cycle of handcycling was defined as one rotation of the crank, starting at the position where the crank was parallel to the propulsion surface and the handle bar aimed towards the person sitting on the handbike (Fig. 1). In wheelchair propulsion, the propulsion cycle was defined as the combination of the push and the recovery phase. The push phase was defined as the time period where the hand exerted a positive torque around the wheel axis. The period where the hands went back to the starting point of the push was defined as the recovery phase. To reduce model calculation time, all input data were re-sampled to 50 Hz and filtered with a second order low-pass Butterworth filter with a cut-off frequency of 10 Hz.
The mean and peak glenohumeral contact force and muscle forces per cycle were calculated and subsequently averaged over the 5 consecutive propulsion cycles.
A Wilcoxon signed-rank test was performed to test whether the power output during handbike and wheelchair propulsion was identical. The power output at the highest level differed significantly between handbike and wheelchair propulsion (Table II). To account for this difference, a linear mixed model, which included power output as a covariate (random effect), was used to analyse the influence of the propulsion device on the shoulder load (mean and peak glenohumeral contact force and relative muscle forces). The fixed effect factor used in the model was the device (handbike vs wheelchair). Level of significance was set at p < 0.05.
| Table II. Measured power output (PO) for wheelchair and handbike propulsion at each level and outcomes of the Wilcoxon signed-rank test |
| Level | 25 W Mean (SD) | 35 W Mean (SD) | 45 W Mean (SD) | 55 W Mean (SD) |
| POhandbike [W] | 26.5 (3.2) | 35.7 (4.2) | 44.9 (4.0) | 52.8 (4.3) |
| POwheelchair [W] | 29.5 (3.2) | 39.3 (3.8) | 48.6 (4.5) | 58.2 (4.8) |
| p | 0.050 | 0.099 | 0.158 | 0.028* |
| *Significant differences in PO between handbike and wheelchair propulsion, p < 0.05. SD: standard deviation. |
Results
Glenohumeral contact force
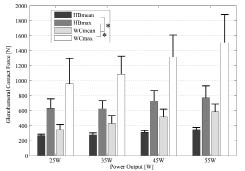
Joint loading, expressed as the glenohumeral contact force, was significantly lower for handcycling than for wheelchair propulsion at all power output levels (p < 0.001) (Fig. 2).
Fig. 2. Mean and peak glenohumeral contact forces and standard deviations of wheelchair (WC) and handbike (HB) propulsion at different power output levels (n = 8). *Significant difference between wheelchair and handbike at all levels, p < 0.001.
At the least straining condition of 25 W, which represents an everyday condition for wheelchair propulsion, the mean glenohumeral contact force was 268 N for handcycling, whereas for wheelchair propulsion a mean glenohumeral contact force of 347 N (+29%) was measured.
At the most straining condition (55 W), the mean value of the glenohumeral contact force during handcycling was 345 N. During wheelchair propulsion in the same condition, a mean glenohumeral contact force of 585 N was measured, which is 70% higher than during handcycling. The differences of the peak values were even more pronounced, with 773 N during handcycling and 1510 N during wheelchair propulsion.
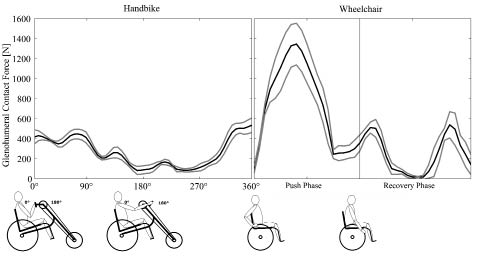
The glenohumeral contact forces during handcycling were evenly distributed over the propulsion cycle, with the highest forces measured around the end of the cycle. This is at the point where the crank was aiming towards the subject (Fig. 3). During wheelchair propulsion, a distinct peak of glenohumeral contact force was measured in the middle of the push phase and smaller peaks were identified at the start and at the end of the recovery phase (Fig. 3).
Fig. 3. Typical example (subject 5) of the glenohumeral contact forces over one propulsion cycle at a power output of 55 W for both handcycling and wheelchair propulsion. Standard deviations are shown in grey.
Muscle force
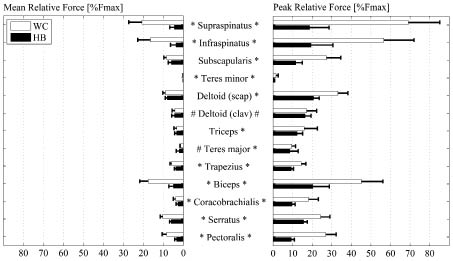
This study showed that, for each of the power output levels, the relative muscle forces were lower during handcycling compared with handrim wheelchair propulsion. The analysis of individual muscles showed that the mean and peak relative muscle forces were lower during handcycling for the majority of the shoulder muscles (p < 0.001), as shown in Fig. 4. The exceptions were the clavicular part of the deltoid (p < 0.001) and the teres major (p < 0.001), which produced more relative muscle force during handcycling. No significant differences were found for the mean values of the subscapularis (p = 0.090), the scapular part of the deltoid (p = 0.343) or the triceps (p = 0.291) (Fig. 4). The highest difference in muscle force between the two propulsion devices was found in the supraspinatus, the infraspinatus and the biceps. The peak values of the biceps and supraspinatus muscle, respectively, were 2.3 times and 3.3 times higher during wheelchair propulsion at 55 W compared with handcycling (Fig. 4).
Fig. 4. Mean and peak relative muscles forces and standard deviations at a power output of 55 W (n = 8), calculated by the Delft Shoulder and Elbow Model. Significant difference between wheelchair (WC) and handbike (HB) over all levels (p < 0.001); *handbike < wheelchair; #handbike > wheelchair.
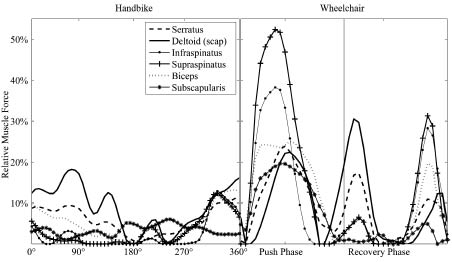
In handcycling, the muscles produce force over the whole propulsion cycle and are recruited in a balanced manner (Fig. 5). In contrast to handcycling, some of the shoulder muscles are used much more during wheelchair propulsion. High muscle forces were produced during the push phase, as well as at the start and the end of the recovery phase. In the push phase and towards the end of the recovery phase, the supraspinatus and infraspinatus were most active. At the beginning of the recovery phase, the most active muscles were the scapular part of the deltoid and the serratus anterior (Fig. 5).
Fig. 5. Typical example (subject 5) of muscle forces over one propulsion cycle at a power output of 55 W. Muscle forces were calculated by the Delft Shoulder and Elbow Model.
Discussion
The clinical purpose of this study was to determine whether the handbike is favourable for the prevention of shoulder problems in persons with SCI. Multiple factors related to propulsion can influence the risk of overuse injuries to the shoulder, such as the amount and direction of the force acting on the joint, the unbalanced use of shoulder muscles or the joint orientation during activity. The present study concentrated on the comparison of glenohumeral contact force and relative muscles forces experienced during handbike and wheelchair propulsion. As expected, the results showed that the shoulder load was lower in handcycling compared with handrim wheelchair propulsion.
Glenohumeral contact force
Both mean and peak glenohumeral contact force were considerably lower during handcycling than during wheelchair propulsion. Due to the continuous force application, the applied force and thus the glenohumeral contact force were more evenly distributed over the whole propulsion cycle. As found in a previous study on able-bodied subjects (11), the peak glenohumeral contact force occurred around the point where the crank was aiming toward the subject (Fig. 3). At this point, the crank had to be lifted against gravity. In addition, the distance from the shoulder to the handgrip was small, which resulted in a smaller shoulder moment arm with which the propulsion force had to be produced. To produce the required external force, more muscles were active during this phase during than the rest of the propulsion cycle (Fig. 5). The sum of these muscle forces resulted in increased glenohumeral contact force.
The mean and peak glenohumeral contact forces found in this study were slightly lower than reported in a previous study on able-bodied subjects (11). The fact that the persons participating in this study were all well-trained handbike users, and might have had a better propulsion technique and coordination, might account for that difference. Also, in wheelchair propulsion the measured glenohumeral contact forces were lower than in comparable studies (12). The pattern of glenohumeral contact force, however, was the same (12). The high peak values found in handrim wheelchair propulsion compared with handcycling resulted from the intermittent force application. All propulsion force had to be applied during the short time of the push phase, which was 55% of the whole propulsion cycle in this study. This inevitably resulted in higher mean and peak values of the applied force, which led to higher glenohumeral contact forces than found during handcycling. The short time of force application goes along with a high rate of rise of the propulsion force, which has been associated with a higher risk for joint injuries (27).
There were also two smaller peaks of glenohumeral contact force during the recovery phase of wheelchair propulsion, where no force was applied to the pushrim. The first peak occurred at the beginning of the recovery phase, where the movement of the arm changed from flexion to extension (Fig. 3). At this point, the scapular part of the deltoid and the serratus were most active and contributed to the high glenohumeral contact force peak (Fig. 5). The second peak occurred at the end of the recovery phase, where the extension movement stopped and the hands were brought back to the starting position of the next push (Fig. 3). At this point, the infraspinatus and supraspinatus were most active (Fig. 5). Between these peaks, when the hands were swinging back, almost no glenohumeral contact force was present. The pattern of glenohumeral contact force during recovery phase might depend on the propulsion style used (28). Performing a circular style, where the hands are swinging back to the starting point below the rim, will probably result in lower peak glenohumeral contact forces than returning to the start of the push with the hands moving back over the rim (single loop over propulsion).
Summarizing the results from a clinical perspective, the higher mean, and especially the higher peak glenohumeral contact forces, found during handrim wheelchair propulsion point to a higher risk for overuse injury, since the repetitive, high forces acting on the shoulder joint have been associated with injuries of the shoulder joint (29, 30).The higher glenohumeral contact forces during wheelchair propulsion resulted from the intermittent force application, and the associated high rate of rise is a further risk of joint injuries (27).
Muscle force
The magnitude and time-series of the relative muscle forces were in accordance with previous studies of handcycling (11, 31–33) and handrim wheelchair propulsion (12, 34).
Comparing the two devices, the relative muscle forces were lower in handcycling than in handrim wheelchair propulsion. During handcycling, the load was spread over all muscles involved; they produced a relative muscle force less than 10% of its maximal value. During wheelchair propulsion, however, some of the muscles were relatively highly stressed. The highest difference of relative muscle force between the 2 devices was found in the supraspinatus (20.7% vs. 4.5%) and infraspinatus (16.5% vs. 3.7%; Fig. 4), which are both part of the rotator cuff. The function of the rotator cuff muscles is to maintain a congruent contact between the humeral head and the glenoid by producing a compressive force component such that the contact force is directed inside the glenoid surface, preventing subluxation, whilst contributing to the necessary shoulder torques (35). If the contribution of rotator cuff muscles is hampered by dysfunction or fatigue, the humeral head can translate superiorly due to insufficient compensation of external forces or the force components of prime movers such as the deltoid or pectoralis. It has been hypothesized that an excessive superior humeral head translation, and its accompanying narrowing of the subacromial space, will lead to subacromial impingement syndrome (36), which is the most common disorder in the shoulder joint of wheelchair-dependent persons (5).
The results of this study showed that the supraspinatus and infraspinatus are more than averagely active during wheelchair propulsion. It is therefore possible that an intensive use of wheelchair propulsion, as it occurs during training and sports, leads to (excessive) fatigue of the rotator cuff muscles and consequently to an increased risk of impingement syndrome. Since the rotator cuff muscles are less stressed during handcycling, this device seems to be a good alternative propulsion mode for preventing this type of overuse injuries.
In conclusion, the shoulder load, assessed as the glenohumeral joint load and the muscular load, was lower in handcycling compared with handrim wheelchair propulsion. Moreover, some muscles of the rotator cuff (infraspinatus and supraspinatus), which are most prone to overuse injuries in wheelchair-dependent persons, were less stressed during handcycling. These results showed that the handbike is a good alternative propulsion mode for outdoor mobility and exercise that might reduce the development of impingement and related problems.
Study limitations
In this study we used a general inverse dynamics model, based on the geometrics of a cadaver. With an individualized model, i.e. by scaling to subject’s dimensions, the calculated forces would be closer to the real forces on the individual level (24). However, on the group level, which was analysed in this study, scaling will not affect the conclusion that the shoulder load is lower in handcycling compared with handrim wheelchair propulsion. To optimize the validity and generalization of the results, subjects with SCI were included who did not have loss of function in the studied muscles due to their lesion level.
The handbike used in this study could not be individually adjusted to each subject, which resulted in different handbike-user interfaces. Thus, the position of the crank with respect to the shoulder was not the same for all subjects, and the moment arm of the forces acting on the shoulder joint, therefore, differed. This could have affected differences in glenohumeral contact forces between individuals. Future studies focusing on the set-up of the handbike with respect to the subject might indicate to what extent the handbike set-up has an effect on shoulder load.
If the SmartWheel did not fit the subject’s own wheelchair, the subjects used the wheelchair from the laboratory, which was not fitted to the subjects. A secondary analysis showed, however, that the subjects using the laboratory wheelchair did not experience different glenohumeral contact forces or muscle forces compared with subjects using their own wheelchair.
The force sensor was attached to the left handgrip of the handbike; therefore, the applied forces were measured only on the left-hand side during handbike and wheelchair propulsion. We assumed the forces applied by the left and right hands to be equal, since Boninger et al. (37) showed that forced measured on the left- and right-side of the wheelchair were highly correlated. This will also apply to the handbike, since the subject propelled straight on the treadmill using synchronous cranks.
The achieved power output was not identical between handbike and wheelchair propulsion. The cause is probably related to the sitting position. The sitting position during handcycling is fixed and is therefore the same during the drag test and during handcycling. Thus, the position of the centre of mass does not change and the drag force to overcome is constant. The sitting position during wheelchair propulsion is more variable and might not be the same during the drag test and during the actual propulsion test (15). This resulted in a difference between the intended and the achieved power output. We corrected for the effect of power output in our statistics, where we included power output as a covariate.
AcknowledgementS
The authors would like to thank Inge Eriks Hoogland, MD, and Matthias Strupler, MD, for the physical examination of the participants, Matthias Schlüssel and Patrizia Marchetto for their help with the data collection, and Veronika Lay for her assistance with the statistical analyses.
References