OBJECTIVE: To evaluate the effects of wheelchair seat height on wheeling efficiency and technique during rehabilitation in subjects with a spinal cord injury.
DESIGN: Laboratory-based study.
SUBJECTS: Twelve persons with spinal cord injury (age range 19–77 years, lesion level: C5/C6–L2; 7 men; 8 incomplete).
METHODS: Subjects conducted 8 submaximal hand rim wheelchair exercise tests (4 min) on a computerized ergometer at 8 seat heights (elbow angle: 70–140°, full extension = 180°) in a counter-balanced order (individualized fixed power output (5.4–13.9 W) and speed). Last-minute physiological and technique parameters were evaluated using repeated measures analysis of variance (ANOVA) and multilevel regression analysis (p < 0.05).
RESULTS: Physical strain and mechanical efficiency changed significantly (p < 0.05) with seat height, with optimal values at 100–130°. Lower seat heights were clearly detrimental. Forces on the hand rims were affected by seat height, showing lower forces with increasing seat height. Lesion level was not a confounder of seat height with respect to mechanical efficiency, oxygen uptake or fraction effective force.
CONCLUSION: Mean physiological data indicate a tendency to optimize at 100–130° seat height. This does not relate to the trends seen in force and technique data. Optimization of seat height during spinal cord injury rehabilitation may lead to more efficient and less straining conditions for manual wheeling.
Key words: physical strain, propulsion technique, anthropometry, mechanical efficiency, force effectiveness.
J Rehabil Med 2009; 41: 143–149
Correspondence address: Lucas H. V. van der Woude, Faculty of Human Movement Sciences, VU University, Van der Boechorststraat 9, NL-1081 BT Amsterdam, The Netherlands. E-mail: lvdwoude@fbw.vu.nl
Submitted February 19, 2008; accepted September 2, 2008
INTRODUCTION
According to Traut (1) wheelchair users sit in their wheelchair for approximately 13.5 h a day. For many individuals the hand rim wheelchair is not only a sitting device, but also a mobility device. The quality and individual fitting of the chair/seat will determine the performance of the wheelchair–user combination, and is crucial for everyday functioning, an active lifestyle, long-term health, individual participation and quality of life (1–3).
Becoming wheelchair-dependent, for example after a spinal cord injury (SCI), often requires the use of a hand rim propelled wheelchair. This implies the use of the relatively small muscles of the arms, shoulders and trunk during almost all activities of daily living (ADL). The energy cost of everyday hand rim wheelchair use appears to be fairly high, as was already noted in the 1960s (4). Janssen et al. (5) stressed the relatively high strain of wheelchair-related ADL. Beyond that, gross mechanical efficiency appears to be in the range of 2–10% under daily use wheeling conditions (6, 7), indicating that 90–98% of the wheelchair user’s oxygen uptake is used for purposes other than for actual wheeled mobility. More recently the mechanical strain of manual wheelchair use and wheelchair-related ADL has been stipulated (8, 9). Van Drongelen et al. (9) showed a high prevalence of shoulder–arm complaints already in early SCI rehabilitation. These early complaints appeared to be predictive of the magnitude of complaints one year after clinical rehabilitation.
It has long been suggested that apart from improving individual physical work capacity and improving the vehicle mechanics of the wheelchair, optimization of the wheelchair–user interface will help reduce the strain of everyday wheelchair use (1, 10). Many different aspects of the wheelchair–user interface have been studied in association with physical strain. Apart from the propulsion mechanism (cranks or levers vs hand rims) (11), different studies evolved around the configuration and orientation of the hand rims (rim size and form, camber angle) and the geometry of the seat (1, 10).
Over time, a considerable series of studies have addressed the effect of (fore–aft and/or vertical) seat orientation on propulsion performance (6, 8, 12–16). The results of these studies in general can be summarized as being rather incongruent, due to differences in methodology, studied population and wheelchair characteristics, as well as the different outcome measures used. For example, Brubaker et al. (17) did find significant relationships between efficiency and seat height-related anthropometric factors for hand rim propulsion. Walsh et al. (18) found no effect of seat position on the peak linear velocity in athletes during wheelchair sprinting in a racing wheelchair. van der Woude et al. (19) studied the effects of anthropometry-related seat height variation on physiology and kinematic parameters. They found significant effects on cardio-respiratory parameters in able-bodied subjects. Mâsse et al. (16) and Hughes et al. (20) studied anthropometry-related seat positions on kinetic parameters, but did not find significant effects. Both Boninger et al. (8) and Kotajarvi et al. (13) found a relationship between axle position and exerted hand force components among wheelchair users. Samuelsson et al. (21) studied seat height effects in subjects with a SCI on gross mechanical efficiency, but despite a trend, found no significant effects.
The studies of van der Woude et al. (19, 22) and Meijs et al. (23) summarize the results of 2 complementary experiments in a group of unimpaired subjects. Based on oxygen uptake and gross mechanical efficiency, the results seem to indicate an optimum seat height of between 100° and 120° elbow angle (seat height being defined as the elbow angle when sitting in a standardized and immobile position with the hands at top-dead-centre of the rim; 180° = full elbow extension; Fig. 1) among a group of non-wheelchair users under steady-state wheeling conditions. Optimum seat height was indicated by increased mechanical efficiency and decreased heart rate and oxygen cost. This does not necessarily indicate an optimum seat orientation with respect to propulsion technique or in terms of mechanical strain, however. Also, it does not imply that experienced wheelchair users comply with the same optimization rules.
Fig. 1. Side view (left panel) of the computerized wheelchair ergometer set-up with graphics of force components and moments that can be derived from the ergometer measurement system (24, 38), as well as the upper and lower arm definition and elbow angle ( ), which was used for seat height adjustment (full extension = 180°). In the right panel typical time tracings of the separate Fx, Fy, Fz force components for 3 subsequent pushes are shown. Fm: tangential force onto the hand rim; M: torque around the wheel axle; Ftot: total force applied onto the hand rim; Fx, Fy, Fz: orthogonal force components of Ftot.
The current study is an attempt to verify seat height effects over a full range of 70–140° elbow angle, using 10° step increments, in a group of persons with SCI. Studying physiological parameters alone, however, is not sufficient to answer the question as to why a particular seat height leads to a lower physiological response. Both kinematic and dynamic push technique parameters may help us to understand variation in physiological parameters among different seat heights. For this reason, in the current study, both kinetic and spatio-temporal technique parameters are studied during submaximal steady state exercise on a stationary computer-controlled wheelchair ergometer.
The objective of this study was to analyse the effects of anthropometry-related seat height variations on physiological and technique parameters during wheelchair propulsion on a computer-controlled wheelchair ergometer during rehabilitation in a group of subjects with a recent SCI.
METHODS
Subjects
Twelve persons (5 women, 7 men) with a recent SCI participated in this study on a voluntary basis. At the time of experimentation subjects were being clinically treated in the Rehabilitation Center Amsterdam. Prior to experimentation, subjects were screened by the physician for contra-indications. The range of lesion level was C5/C6–L2 and age range 19–77 years. Table I shows personal and anthropometric data.
This study was approved by the local ethics committee. All subjects gave their written informed consent.
| Table I. Personal and lesion characteristics for 12 subjects with spinal cord injury during rehabilitation |
| | Age, years, Gender | Weight, kg | Lesion level, c/ic | Bi-acromial width, m | Upper arm length, m | Lower arm length, m |
| | 21/F | 47.0 | L1, ic | 0.327 | 0.285 | 0.269 |
| | 19/M | 65.0 | C5/6, c | 0.393 | 0.36 | 0.319 |
| | 29/M | 70.0 | L1/2, c | 0.384 | 0.322 | 0.293 |
| | 57/F | 49.0 | C7, ic | 0.289 | 0.32 | 0.263 |
| | 29/F | 38.5 | L1, ic | 0.365 | 0.296 | 0.253 |
| | 64/M | 76.0 | L2, ic | 0.378 | 0.339 | 0.283 |
| | 38/M | 102.5 | L1, c | 0.368 | 0.355 | 0.301 |
| | 45/F | 94.0 | C6/7, ic | 0.36 | 0.314 | 0.263 |
| | 24/M | 66.0 | C7, ic | 0.395 | 0.394 | 0.297 |
| | 48/M | 64.0 | C7, c | 0.378 | 0.334 | 0.288 |
| | 77/F | 67.0 | Th8, ic | 0.354 | 0.322 | 0.255 |
| | 50/M | 64.0 | C6, ic | 0.341 | 0.347 | 0.291 |
| Mean (SD) | 41.8 (18.3) | 66.9 (18.2) | – | 0.361 (0.030) | 0.332 (0.030) | 0.281 (0.021) |
| c: complete lesion; ic: incomplete lesion; L1: lesion level: F: female; M: male; SD: standard deviation. |
Protocol
To evaluate the effect of seat height upon physiological and technique data, 8 randomly ordered submaximal tests at 8 different seat heights were conducted on a computer-controlled wheelchair ergometer (Fig. 1) (24). Seat height was adjusted relative to body dimensions with the help of the elbow angle, and set up with steps of 10° from 70° to 140° elbow angle (full extension = 180°; during seat height adjustment, the subject sits upright with the hands on top-dead-centre (12 o'clock) of the hand rim; the elbow angle is determined and indicative for seat height (Fig. 1) (19, 22, 23). Each test began with a warm-up period of 5 min at a given seat height, followed by a 4-min exercise bout at the designated resistance and speed. After this, a 5-min rest period preceded the next warm-up period at a different seat height was conducted. Subjects received continuous feedback on their speed and the required test speed via a computer screen.
Because of the variation in physical capacities within the group, 5 different exercise intensity protocols were eventually defined, based on power output (PO) estimates of Janssen et al. (25) and individual characteristics. These experimental conditions were individually defined in terms of power output (PO: 5.4 –13.9 W; based on simulation of rolling resistance, slope (0.25–0.5°) and speed (0.42–0.83 m/sec. Inertia of the wheels was dependent on body weight and the weight of the virtual wheelchair (15 kg). These were used as control variables for the computer-controlled ergometer.
In the warm-up period, one of the 5 exercise intensities was chosen for each individual subject, based on the apparent performance capacity of the subject. Exercise intensity, slope and speed, were kept constant for each subject over the 8 different exercise bouts (and thus seat heights). During the resting period following each test the subjects were asked to give their opinion about the effort of propulsion at that specific seat height (scale: 1 = very easy, to 5 = very heavy).
Ergometer
The stationary adjustable computer-controlled wheelchair ergometer (24, 26) enabled the analysis of momentary 3-dimensional (3D) force of the hand on the hand rim together with the torque around the wheel axis during standardized exercise testing and in conjunction with cardio-respiratory measures (Fig. 1). Together with the momentary velocity, peak and mean power output can be derived. The camber of the wheels was set at 4°. Seat angle was fixed to 5° inclination, the backrest was fixed to 10° inclination. The fore–aft position of the seat was fixed individually with the subject's acromion vertically above the wheel axle. Wheel and hand rim diameter were 0.62 and 0.52 m, respectively. The size of the rim tube was 0.03 m. Distance between the wheels was set proportional to bi-acromial width. In 8 cases the distance had to be increased because otherwise the special cushion of the subjects would have influenced the measurements of the force transducers. Over the different seat height conditions, individual ergometer settings other than seat height were kept constant.
Physiological data
Expired gases were collected with an Oxycon (Ox-4, Mijnhardt, Breda, The Neatherlands) continuously during each exercise block. Every 30 sec the average values over 30 sec of the respiratory parameters were processed. The mean of the data of the last minute of each exercise block was used. The Oxycon was calibrated before each experiment with known reference gas mixtures. Minute ventilation ((VE); Body Temperature Pressure Saturated (BTPS), l/min), oxygen uptake ((VO2); Standard Temperature Pressure Dry (STPD), l/min), carbon dioxide output ((VCO2); STPD, l/min) and respiratory exchange ratio (RER) were determined. Heart rate was continuously measured with a sport tester PE4000 (Polar, Kempele, Finland). The gross energy cost (Egross; kJ) was calculated according to the method described by Péronnet & Massicotte (27). Gross mechanical efficiency (ME) was derived from the ratio between mean external power output and Egross. The mean power output (PO) was calculated for the left and right side of the ergometer separately according to the following equation:
PO = M × Vw / Rw (W) (1)
where M is the propulsion torque in Nm (Fig. 1), Vw is the wheel velocity in m/s and Rw is the radius of the wheel (0.31 m). Mean PO is the average power output over time and the sum for both wheels.
Technique data
In the last minute of each exercise block the ergometer data were sampled at 100 Hz synchronously with the physiological data for a period of 15 sec. Torque applied to the hand rims was measured at both sides, as was the velocity of the wheels. The forces on the hand rims were registered in 3 directions, but only on the right-hand side. The data were filtered using a 4th-order recursive low-pass Butterworth filter with a cut-off frequency of 8 Hz for Fx, Fz, M and velocity. For Fy the cut-off frequency was 5 Hz. The force component directed horizontally in the plane of motion was defined as Fx (forward = positive), horizontally, but perpendicular to the plane of motion as Fy (outward = positive) and vertically in the plane of motion as Fz (downward = positive). The total force produced onto the hand rim (total force vector (Ftot)) was determined from 3D components Fx, Fy and Fz according to the following equation:
Ftot = √(Fx2 + Fy2 + Fz2) (N) (2)
The effective or tangential force (Fm) on the hand rim was calculated from torque (M) and rim radius (Rr; 0.26 m), according to the following equation:
Fm = M / Rr (N) (3)
From equations 2 and 3 the “fraction effective force” (FEF; (26)) is calculated, which is the ratio between the total force produced and the effective or tangential component that contributes to the actual PO:
FEF = Fm / Ftot × 100 (%) (4)
FEF was expressed as the percentage of mean values of Fm and of Ftot over each push.
Dip is the mean of the negative deflection in the effective force (Fm) curve at the start of the push in N, it is a typical brief braking force at the start of the push. The peak values of the force components (Ftotpeak, Fxpeak, Fypeak, Fzpeak) within a push for the right side were averaged over a minimal number of 9 pushes. The peak torque of each push (Mpeak) right side respectively were also calculated. Push time (PT) is the duration of the push phase (hand-to-rim contact) in sec, and was derived from the force data.
Statistical analysis
An analysis of variance for repeated measures was conducted on main factor seat height (SPSS-12; SPSS-Inc, Chicago, Illinois, USA). Differences were considered significant at p ≤ 0.05. To evaluate the combined effects of seat height, the role of lesion level (tetraplegia = 1; paraplegia = 0) and variation between subjects in power output on the outcomes ME, VO2 and FEF, a multilevel regression analysis was conducted (MlwiN 2.0; Center for Multilevel Modelling, University of Bristol, UK).
RESULTS
Subjects and protocol
Due to limitations in the wheelchair ergometer in association to the special cushioning required for some subjects, it was not possible to test all 8 seat heights in all subjects. The lowest seat height (70°) and the highest seat height (140°) were not evaluated in 9 and 5 subjects, respectively. Analysis was limited therefore to the seat height range of 80–140° elbow angle, where missing values for 5 subjects at 140° were substituted using the individual mean of the other available seat height results for an individual. Exercise intensity varied among subjects (5.4–13.9W), but remained constant within subjects over the different seat height conditions.
Physiological data
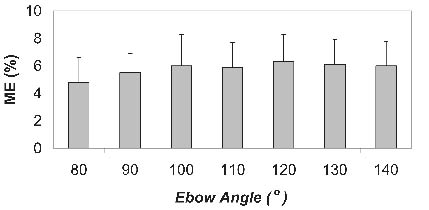
Table II presents the mean (standard deviation (SD)) physiological outcome parameters (n = 12) obtained for the different seat height conditions. Mean RER values indicate that the experiments were submaximal in general. ME for all seat heights is low, with 6.3% at 120° being the group peak value. For VE, VO2, and Egross the absolute minimum values at group level are seen at 130°. All physiological data except power output show significant effects with seat height (p ≤ 0.05). Visual inspection of the data showed that wheelchair propulsion at 80° and 90° are clearly less efficient than at the other higher seat positions, with a tendency to optimize at group level within the range 100–130° (Fig. 2).
Fig. 2. Gross mechanical efficiency (ME) for 12 subjects with a spinal cord injury (mean (standard deviation) in association with seat height (expressed as elbow angle; full extension = 180°).
Multilevel regression analysis with VO2 and ME as dependent variables showed that neither lesion level nor PO was a significant confounder in the association between seat height and either of the 2 outcomes. The final multilevel equation (showing regression coefficients (± standard error) for the different independent parameters) with mechanical efficiency as dependent parameter, was:
ME (%) = 2.39 (1.138) + 0.018 (0.009) Seat height – 0.61 (0.48) Lesion level + 0.18 (0.08) PO
This showed significant effects of seat height and PO on ME and not lesion level (similar results were found for the dependent parameter VO2); thus, based on the current preliminary data, the effect of lesion level is primarily an effect of differences in power output for the 2 lesion groups.
Technique data
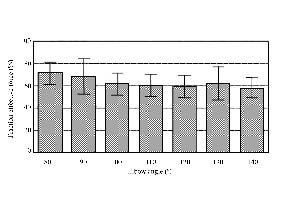
As shown in Table III, group results showed significant effects of seat height on the FEF and total force applied (Ftotpeak) (p < 0.05). The highest value for Ftotpeak is reached at 120° (Fig. 3). In contrast to mechanical efficiency, FEF decreased more or less linearly with increasing seat height and drops from a mean 71% at 80o to 58% at the 130° seat height condition. Negative deflection at start of a push decreased significantly with increasing seat height, while push time (PT) (p = 0.053) and peak torque remained constant with increasing seat height.
Fig. 3. Mean (standard deviation) fraction effective force for 12 subjects with a spinal cord injury at different seat heights (80–140°).
Multilevel regression analysis again showed that neither lesion level nor PO was a confounder in the relationship between FEF and seat height. Seat height, lesion level and PO were all significant determinants of FEF:
FEF (%) = 76.9 (7.9) – 0.19 (0.05) Seat height –7.6 (2.77) Lesion level + 1.1 (0.45) POmean
The above equation suggests a drop in FEF of 1.9% with each 10° increase in seat height, a 7.6% lower FEF is seen for those with tetraplegia, while a 1 W higher power output would lead to an increase in FEF of 1.1%.
DISCUSSION
Subjects and protocol
All the persons with SCI treated at the Rehabilitation Centre Amsterdam at the time of the experiment were invited to participate in this study. This led to an expected inhomogeneous group (lesion characteristics, work capacity, anthropometry, etc.).
The data of the lowest seat height, 70°, could not be analysed because data of only 3 subjects were available due to limitations of the geometry of the ergometer. Of those few results, it could be derived that metabolic cost at 70° would indeed have further increased compared with the 80° and 90° conditions.
Despite a conservative choice for exercise intensity, the overall protocol (8 consecutive seat height conditions in one session) appeared quite strenuous. The heart rate data showed a slight tendency to increase with the increasing number of tests. Therefore, the resting heart rate just prior to a trial was determined and used to correct the mean heart rate during the last minute of that trial (∆ HR; Table II). Consequently, all data were re-analysed for a possible sequence effect, but were non-significant.
| Table II. Mean (SD) results (n = 12) obtained at different seat heights (expressed in degrees elbow angle; 180° = full extension; ANOVA: main effects of repeated measures ANOVA for seat height (*p ≤ 0.05) |
| Seat height | 80° | 90° | 100° | 110° | 120° | 130° | 140° | ANOVA p < 0.05 |
| ME, % | 4.8 (1.8) | 5.5 (1.4) | 6.0 (2.3) | 5.9 (1.8) | 6.3 (2.0) | 6.1 (1.8) | 6.0 (1.8) | * |
| VE, l/min | 20.1 (6.1) | 17.9 (5.1) | 15.7 (4.7) | 14.6 (3.5) | 15.5 (4.9) | 14.0 (4.7) | 16.9 (5.0) | * |
| VO2, l/min) | 0.57 (0.18) | 0.51 (0.15) | 0.48 (0.15) | 0.45 (0.11) | 0.46 (0.15) | 0.42 (0.15) | 0.47 (0.15) | * |
| RER | 0.92 (0.10) | 0.88 (0.09) | 0.86 (0.06) | 0.83 (0.05) | 0.84 (0.06) | 0.85 (0.06) | 0.89 (0.10) | * |
| ∆ HR | 24 (6) | 21(6) | 19 (7) | 16 (7) | 18 (6) | 18 (7) | 15 (6) | * |
| Egross, kJ | 12.2 (3.9) | 10.8 (3.4) | 9.9 (3.3) | 9.5 (2.2) | 9.6 (3.1) | 9.0 (3.1) | 10.0 (3.0) | * |
| PO, W | 9.5 (3.4) | 9.7 (3.0) | 9.4 (3.4) | 9.1 (2.8) | 9.5 (3.1) | 9.0 (3.6) | 9.6 (3.1) | – |
| SD: standard deviation; ME: mechanical efficiency; VE: ventilation; VO2: oxygen uptake; RER: respiratory exchange ratio; ∆ HR: heart corrected for resting heart rate just prior to the exercise bout; Egross: energy cost; PO: mean power output; ANOVA: analysis of variance. |
Physiology
Despite the heterogeneous group, significant curvi-linear effects with seat height were found in all physiological parameters (VO2, ME, VE, RER, HR, Egross) indicating the relevance and possibility of optimizing wheelchair seat height on the basis of elbow angle at group level. Mean results (Table II) among the current 12 subjects with a SCI showed a possible 1.5% absolute gain in mechanical efficiency through the optimization of seat height (i.e. a 25% relative gain at an individual ME of 6%). This is clearly a meaningful change given the low overall work capacity of SCI. Seat height optimization must be included in wheelchair set-up guidelines in rehabilitation.
Most studies on seat height did not find significant effects on the selected outcome measures (6, 16, 18, 20); this is, however, in contrast with the current results and those of van der Woude et al. (19, 22) and Meijs et al. (23). Differences in outcome measures as well as the methodology of seat height adjustment may have contributed to the inconsistency of published results. The choice for elbow angle as a measure for seat height, and the overall standardization of the ergometer set-up to individual anthropometric characteristics in the current study takes into account inter-individual variation (in trunk, and arm segment lengths, and width), yet leads to a standardized seat height set-up. Seat height in most studies was not standardized according to anthropometric dimensions (18). Although Hughes et al. (20) and Mâsse et al. (16) used standardized seat heights based on arm and trunk lengths in a group of wheelchair users, they studied biomechanical parameters and no cardio-respiratory parameters. Samuelsson et al. (15) studied effects of 2 different seat heights in a group of 25 subjects with SCI during submaximal wheeling on a motor driven treadmill. Seat height affected weight distribution and seat inclination angle, which in turn affected push frequency and stroke angle. No effects were seen on mechanical efficiency. On the treadmill seat position variation may affect rolling resistance, which may counteract any seat position effect present. The computer-controlled ergometer allows full isolation of variation in seat dimensions from rolling friction or power output. In daily life seat height variation leads to toe-in or toe-out (misalignment of) of cambered rear wheels, which affects rolling resistance considerably (28). Obviously, this misalignment must be compensated for in the frame set-up.
Combined data of Meijs et al. (23) and van der Woude et al. (19, 22) reported more or less identical trends of varying seat height at 2 submaximal levels of PO, showing optimal levels of ME at elbow angles between 100° and 120°. This effect is suggested to be associated with changes in length-tension (and possibly force-velocity) characteristics of individual muscles involved (19, 22, 23). The current results corroborate these results for SCI. When considering group results, 80° and 90° seat heights are clearly less efficient than the other higher seat heights. The seat heights 100–140° do not show large differences despite a tendency to optimize between 100° and 130°. Lesion level had no confounding effect on the correlation between ME or VO2 and seat height. However, in those with a tetraplegia, ME was 1.3% lower. Adding PO to the multilevel equation, however, overruled the lesion level effect, indicating that lesion level effects can be attributed to differences in PO between those with tetraplegia and paraplegia.
Propulsion technique
Apart from an optimal cardio-respiratory strain and mechanical efficiency in hand rim propulsion, there is the need for reduction of upper extremity mechanical loading. People with SCI indeed have a high risk of mechanical overuse of the shoulders and wrists (9). External force of the hands on the hand rim is indicative for mechanical load on the joints. The current study showed significant effects of seat height on peak fraction effective force, the peak total force, and negative deflection at the start of the push (Table III) with tendencies for peak forces to increase with a higher seat height. PT and peak torque were not significantly affected by seat height, although PT showed a trend (p = 0.053) with increasing seat height.
| Table III. Mean (SD) results (n = 12) obtained at different seat heights (expressed as degrees elbow angle; 180° = full extension). Means within rows with different superscripts differ significantly; ANOVA: main effects of repeated measures ANOVA for seat height (*p ≤ 0.05) |
| Seat height | 80° | 90° | 100° | 110° | 120° | 130° | 140° | ANOVA p < 0.05 |
| FEF, % | 71 (10) | 68 (16) | 62 (9) | 60 (10) | 59 (10) | 62 (15) | 58 (9) | * |
| PT, sec | 0.59 (0.20) | 0.64 (0.23) | 0.65 (0.22) | 0.63 (0.15) | 0.57 (0.16) | 0.60 (0.18) | 0.56 (0.16) | – |
| DIP, N | –3.6 (1.3) | –3.1 (1.2) | –3.1 (1.9) | –2.8 (1.7) | –3.5 (1.8) | –2.6 (1.4) | –2.6 (1.1) | * |
| Ftotpeak, N | 44.2 (9.9) | 48.3 (10.5) | 48.0 (10.2) | 49.2 (11.3) | 54.8 (14.7) | 48.7 (11.7) | 54.4 (9.3) | * |
| Fxpeak, N | 24.9 (5.8) | 28.2 (8.3) | 27.6 (6.1) | 26.7 (6.8) | 28.5 (6.2) | 26.9 (5.7) | 29.1 (5.4) | – |
| Fypeak, N | 4.6 (3.7) | 4.6 (3.8) | 3.8 (2.9) | 6.8 (5.3) | 7.4 (6.0) | 6.2 (5.7) | 7.9 (3.8) | * |
| Fzpeak, N | 38.4 (10.2) | 40.9 (9.3) | 39.0 (10.9) | 42.7 (10.2) | 48.0 (14.6) | 41.4 (11.7) | 46.4 (9.6) | * |
| Mpeak, Nm | 9.63 (3.2) | 9.04 (2.5) | 8.57 (2.6) | 8.32 (2.2) | 8.9 (2.3) | 7.89 (2.1) | 8.96 (2.3) | – |
| FEF: fraction effective force; PT: push time; DIP: negative deflection at start of a push; Ftotpeak: peak total force applied; Fxpeak: peak force (forward = positive), Fypeak: peak medio-lateral force (outward = positive); Fzpeak: vertical peak force (downward = positive); Mpeak: peak torque around the wheel axle (see Fig. 1); ANOVA: analysis of variance; SD: standard devition. |
Different biomechanical studies have evaluated the effects of seat height on different temporal-spatial, kinematic, muscle and/or kinetic parameters (8, 13, 14, 16, 20, 22, 23, 29, 30), but there is little support for the findings in the current study. Kotajarvi et al. (13) studied 9 wheel axle (fore–aft and height) positions (not adjusted for different anthropometrics) during overground propulsion (and at self-selected speed) on kinematic and kinetic parameters in 13 experienced wheelchair users. They found significant effects on PT and radial and axial forces with a shorter distance between shoulder and wheel axle. In contrast, FEF and tangential force did not change with seat position (13). Again, prudence is required with interpretation of these data, since differences in rolling friction with different sitting positions may have confounding effects. Wei et al. (30) showed significant effects of seat height on temporal and wrist kinematics among a group of 11 wheelchair users. Both Wei et al. (30) and Kotajarvi et al. (13) did not normalize seat height to the individual anthropometry. Self-selected speed may have introduced another confounding effect. Studies of Mâsse et al. (16), Hughes et al. (20) and Meijs et al. (23) showed significant effects of seat height on muscle activation and/or kinematics of the upper extremity among wheelchair users and able-bodied subjects. In a kinetic analysis Boninger et al. (8) showed associations between push angle and the vertical axle position in 40 wheelchair users with paraplegia during submaximal steady state wheeling bouts and a brief wheelchair sprint, but not on other outcome measures. Again, there is considerable inconsistency among the studies in methods employed and standardization of testing conditions.
In 1989, van der Woude et al. (22) evaluated both physiology and kinetics of 3 different seat heights (70–90° elbow angle; 2 levels of power output) in a group of 5 male able-bodied subjects. Although they found significant effects on oxygen uptake with seat height, no effects on peak torque, work per cycle, PT or any of the other studied technique parameters were found. In contrast, van der Woude et al. (19) found a lower PT with increasing seat height. In the current study shifts in PT were small (p = 0.053), showing highest values in the range of 90–110°. A higher PT implies a lower stroke frequency and longer strokes, which is suggested to be less straining (8). Similarly, a decrease in peak hand force is suggested to be beneficial. van der Woude et al. (22) suggested that FEF drops with increasing seat height and that this will influence the energy cost.
FEF values in the current study were in line with literature (26). As suggested by van der Woude et al. (22), current results indeed indicate a decrease in FEF with seat height, a trend almost inversely linked to ME. A similar inverse association between ME and FEF was seen in previous hand rim learning studies of de Groot et al. (31, 32) and Kotajarvi et al. (13), as well as in cycling (33). Also, biomechanical modelling suggests FEF in hand rim wheelchair propulsion to be optimally organized from a biological perspective; it cannot simply be increased intentionally through training (34). An optimal direction of hand force in mere mechanical terms is evidently the force directed tangential to the rim radius. Within that context, the current FEF data indicate a less effective direction of the force overall and a decrease with increasing seat height. Optimization of the power contribution of shoulder and elbow muscles as well as the prevention of a conflict between flexor and extensor muscles (co-contraction) around the elbow seem to be responsible (26, 34, 35). With increasing seat height the arm-trunk geometry will lead to changes in relative moment arms towards a larger shoulder moment arm to allow proper coupling of the hand to the hand rim as well as to secure the production of sufficient work onto the rim with each push. A drop in FEF with seat height associates with a higher Ftotpeak, while the tangential force Fm remains constant (Table III) and ME shows an inverse trend. Simply improving ME does not necessarily optimize force application characteristics, while the reverse is probably also true. How FEF variation impacts on joint reaction forces requires evaluation in model-based full joint kinetic studies (35–37), preferably combined with metabolic measures.
In conclusion, at group level, and based on cardio-respiratory parameters and mechanical efficiency, subjects with SCI during rehabilitation showed an optimal seat height over a range of 100–130o elbow angle (defined in a standardized sitting posture) during submaximal hand rim wheelchair propulsion. With the highest seat heights, mechanical loading seems to increase in terms of FEF and external peak hand forces. Rehabilitation professionals must be aware of the importance of fine-tuning of the wheelchair-user interface to the individual and its underlying consequences for functioning and (future) health. It is advisable to monitor seat height at the individual level and early in rehabilitation in order to minimize both metabolic and mechanical strain.
ME cannot be explained from changes in FEF; the latter appears to be regulated by the task constraints and the geometry of the arm/shoulder and is not directly linked to efficiency. How external force impacts on reaction force at the joints must be evaluated in future studies.
REFERENCES
1. Traut L. Gestaltung ergonomisch relevanter Konstruktionsparameter am Antriebsystem des Greifreifenrolstuhls -Teil 1-Teil II. Orthopadie Technik 1989; 7, 8: 394–399, 456–460.
2. Lesser W. Arbeitsphysiologische, biomechanische und anthropometrische Untersuchungen an Rollstuhlen. Statuskol 1984; 3: 25–28.
3. McLaurin CA, Brubaker CE. Biomechanics and the wheelchair. Prosthet Orthot Int 1991; 15: 24–37.
4. Voigt ED, Bahn D. Metabolism and pulse rate in physically handicapped when propelling a wheelchair up an incline. Scand J Rehab Med 1969; 1: 101–106.
5. Janssen TW, van Oers CA, van der Woude LH, Hollander AP. Physical strain in daily life of wheelchair users with spinal cord injuries. Med Sci Sports Exerc 1994; 26: 661–670.
6. Brattgard S-O, Grimby G, Hook O. Energy expenditure and heart rate in driving a wheelchair ergometer. Scand J Rehab Med 1970; 2: 143–148.
7. Hintzy F, Tordi N. Mechanical efficiency during hand rim wheelchair propulsion: effects of baseline substractions and power output. Clin Biom 2004; 19: 343–349.
8. Boninger ML, Baldwin M, Cooper RA, Koontz A, Chan L. Manual wheelchair pushrim biomechanics and axle position. Arch Phys Med Rehabil 2000; 81: 608–613.
9. van Drongelen S, de Groot S, Veeger HE, Angenot EL, Dallmeijer AJ, Post MW, et al. Upper extremity musculoskeletal pain during and after rehabilitation in wheelchair-using persons with a spinal cord injury. Spinal Cord 2006; 44: 152–159.
10. Lesser W. Arbeitsphysiologische Untersuchungen des Rollstuhls mit Greifreifenantrieb. Med Orthop Techn 1981; 5: 139–143.
11. Dallmeijer AJ, Zentgraaff ID, Zijp NI, van der Woude LH. Submaximal physical strain and peak performance in handcycling versus handrim wheelchair propulsion. Spinal Cord 2004; 42: 91–98.
12. Engel P, Hildebrandt G. Arbeitsphysiologische Untersuchungen an handbetriebenen Krankenfahrstuhlen mit verschiedenen Antriebsformen. Mot 1976; 2: 28–32.
13. Kotajarvi BR, Sabick MB, An KN, Zhao KD, Kaufman KR, Basford JR. The effect of seat position on wheelchair propulsion biomechanics. J Rehabil Res Dev 2004; 41: 403–414.
14. Mulroy S, Newsam C, Gutierrez D, Requejo P, Gronley J, Haubert L, et al. Effect of fore-aft seat position on shoulder demands during wheelchair propulsion: part 1 A kinetic analysis. J Spinal Cord Med 2005; 28: 214–221.
15. Samuelsson KA, Tropp H, Nylander E, Gerdle B. The effect of rear-wheel position on seating ergonomics and mobility efficiency in wheelchair users with spinal cord injuries: a pilot study. J Rehabil Res Dev 2004; 41: 65–74.
16. Masse LC, Lamontagne M, O’Riain MD. Biomechanical analysis of wheelchair propulsion for various seating positions. J Rehabil Res Dev 1992; 29: 12–28.
17. Brubaker CE, McClay IS, McLaurin CA. Effect of seat position on wheelchair propulsion efficiency. Proceedings of the 2nd International Conference on Rehabilitation Engineering: Ottawa: Canadian Medical and Biological Society; 1984, p. 12–14.
18. Walsh CM, Marchiori GE, Steadward RD. Effect of seat position on maximal linear velocity in wheelchair sprinting. Can J Appl Sport Sci 1986; 11: 186–190.
19. van der Woude LH, Veeger DJ, Rozendal RH, Sargeant TJ. Seat height in handrim wheelchair propulsion. J Rehabil Res Dev 1989 26: 31–50.
20. Hughes CJ, Weimar WH, Sheth PN, Brubaker CE. Biomechanics of wheelchair propulsion as a function of seat position and user-to-chair interface. Arch Phys Med Rehabil 1992; 73: 263–269.
21. Samuelsson K, Larsson H, Thyberg M, Gerdle B. Wheelchair seating intervention. Results from a client-centred approach. Disabil Rehabil 2001; 23: 677–682.
22. van der Woude LH, Veeger DJ, Rozendal RH, Koperdraat J, Drexhage D. Seat height in handrim wheelchair propulsion: a follow-up study. J Rehab Sci 1990; 3: 79–83.
23. Meijs PJM, van Oers CAJM, Veeger HEJ, van der Woude LHV. The effect of seat height on the physiological response and propulsion technique in wheelchair propulsion. J Rehab Sci 1989; 2: 104–107.
24. Niesing R, Eijskoot F, Kranse R, den Ouden AH, Storm J, Veeger HE, et al. Computer-controlled wheelchair ergometer. Med Biol Eng Comput 1990; 28: 329–338.
25. Janssen TW, van Oers CA, Hollander AP, Veeger HE, van der Woude LH. Isometric strength, sprint power, and aerobic power in individuals with a spinal cord injury. Med Sci Sports Exerc 1993; 25: 863–870.
26. Veeger HE, van der Woude LH, Rozendal RH. Effect of handrim velocity on mechanical efficiency in wheelchair propulsion. Med Sci Sports Exerc 1992; 24: 100–107.
27. Péronnet F, Massicotte D. Table of nonprotein respiratory quotient: an update. Can J Sport Sci 1991; 16: 23–29.
28. van der Woude LH, Veeger HE, Dallmeijer AJ, Janssen TW, Rozendaal LA. Biomechanics and physiology in active manual wheelchair propulsion. Med Eng Phys 2001; 23: 713–733.
29. Guo LY, Zhao KD, Su FC, An KN. Moment generation in wheelchair propulsion. Proc Inst Mech Eng [H] 2003; 217: 405–413.
30. Wei SH, Huang S, Jiang CJ, Chiu JC. Wrist kinematic characterization of wheelchair propulsion in various seating positions: implication to wrist pain. Clin Biomech (Bristol, Avon) 2003; 18: S46–S52.
31. de Groot S, Veeger DH, Hollander AP, Van der Woude LH. Wheelchair propulsion technique and mechanical efficiency after 3 wk of practice. Med Sci Sports Exerc 2002; 34: 756–766.
32. de Groot S, Veeger HE, Hollander AP, van der Woude LH. Consequence of feedback-based learning of an effective hand rim wheelchair force production on mechanical efficiency. Clin Biomech (Bristol, Avon) 2002; 17: 219–226.
33. Korff T, Romer LM, Mayhew I, Martin JC. Effect of pedaling technique on mechanical effectiveness and efficiency in cyclists. Med Sci Sports Exerc 2007; 39: 991–995.
34. Rozendaal LA, Veeger HE, van der Woude LH. The push force pattern in manual wheelchair propulsion as a balance between cost and effect. J Biomech 2003; 36: 239–247.
35. Veeger HE, Rozendaal LA, van der Helm FC. Load on the shoulder in low intensity wheelchair propulsion. Clin Biomech (Bristol, Avon) 2002; 17: 211–218.
36. van Drongelen S, van der Woude LH, Janssen TW, Angenot EL, Chadwick EK, Veeger DH. Glenohumeral contact forces and muscle forces evaluated in wheelchair-related activities of daily living in able-bodied subjects versus subjects with paraplegia and tetraplegia. Arch Phys Med Rehabil 2005; 86: 1434– 1440.
37. van Drongelen S, van der Woude LH, Janssen TW, Angenot EL, Chadwick EK, Veeger HE. Glenohumeral joint loading in tetraplegia during weight relief lifting: a simulation study. Clin Biomech (Bristol, Avon) 2006; 21: 128–137.
38. Veeger HE, van der Woude LH, Rozendal RH. A computerized wheelchair ergometer. Results of a comparison study. Scand J Rehabil Med 1992; 24: 17–23.